aprendeconomia

La función de producción muestra la relación existente entre el producto obtenido y la combinación de factores que se utilizan en su obtención, es decir, es la expresión matemática que relaciona las cantidades de factores empleadas con la cantidad de producto obtenido según una técnica determinada. Viene dada por la expresión,  donde:

                                    Q = Cantidad máxima de producto obtenido

                                    T = Tierra

                                    L = Trabajo

                                    K = Capital

                                    E = Iniciativa empresarial

Se puede entender claramente a través de un ejemplo: supongamos que un agricultor se dedica al cultivo del trigo. Utiliza la tierra de que dispone, las semillas, los abonos, los fertilizantes, los trabajadores, los tractores, las máquinas cosechadoras, etc. La función de producción indica al agricultor cuál es el nivel de producción (cantidad de trigo) que alcanzará mediante la combinación de todos los factores productivos de los que dispone en ese momento. La dimensión temporal tiene aquí vital importancia, ya que la función de producción hace referencia a un momento del tiempo en el que la tecnología está dada, puesto que si se produce un cambio tecnológico (que puede ser desde un cambio en la forma de combinar los recursos productivos hasta un avance técnico) la función de producción variará.

Por tanto, a la hora de estudiar la empresa como unidad productora de bienes y servicios debemos tener en cuenta el periodo de tiempo considerado por ésta para adoptar sus decisiones. En este sentido, atendiendo a su dimensión temporal, podemos diferenciar dos perspectivas de producción:

• Producción a corto plazo. Es la que se produce en un periodo de tiempo durante el cual sólo puede variar la cantidad de algunos factores.

• Producción a largo plazo. Es la que se obtiene en un espacio de tiempo durante el cual todos los factores de producción pueden variar.

1. LA PRODUCCIÓN A CORTO PLAZO

Para analizar la producción a corto plazo vamos a utilizar un ejemplo. Supongamos que un grupo de amigos decide montar una pastelería. Los factores productivos necesarios para la producción de pasteles son el trabajo (número de trabajadores a contratar), el capital (un local, hornos, utensilios para hacer pasteles, mobiliario y materias primas) y la iniciativa empresarial necesaria para llevar adelante el proyecto.

Para simplificar el análisis supondremos que sólo se utilizan dos factores productivos: capital y trabajo. En concreto, los amigos han alquilado un local comercial de 200  y dos hornos que constituirán el factor capital, a corto plazo fijo o invariable. Por otro lado, el factor variable será la mano de obra, es decir, el número de trabajadores o de horas de trabajo a contratar. Si se quiere aumentar la producción de pasteles habrá que incrementar la cantidad de factor variable (el trabajo).

De este modo, la función de producción a corto plazo viene dada por la expresión:

 donde:

                                    Q = nivel de output (pasteles) a producir

                                    L = trabajo o factor variable a corto plazo

                                     = capital o factor fijo a corto plazo

La producción semanal que alcanzaría la pastelería a medida que se aumente el factor variable, es decir, según se incorporen trabajadores, se representa gráficamente como sigue:

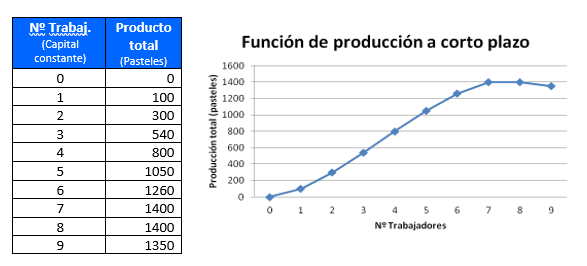
Este gráfico muestra que cuando no hay trabajadores la producción es nula y que, según se van incorporando unidades de trabajo, la producción de pasteles se va incrementando hasta un punto en que no sólo no se incrementa, sino que incluso decrece.

Este fenómeno se debe a la Ley de los rendimientos decrecientes que afirma que si aumenta la cantidad de uno de los factores productivos (el trabajo), pero el resto se mantiene constante (el capital), la producción total aumentará de forma cada vez más lenta hasta dejar de crecer, pudiendo incluso disminuir.

Explicación de la ley: en nuestro ejemplo, el capital físico (el local y los dos hornos) tiene una capacidad de uso limitada y aunque al incorporar los primeros trabajadores los incrementos de producción son importantes debido a que pueden repartirse las tareas entre ellos (amasar, hornear, atender al público, etc.) y especializarse, a partir de un determinado número de trabajadores las posibilidades de dividir el trabajo entre ellos serán menores, lo que provocará la aparición de tiempos muertos e incluso que unos trabajadores estorben a otros, desembocando la situación en un descenso del rendimiento y, posiblemente, de la producción total.

Esta ley sólo se cumple en el corto plazo, ya que existen factores fijos y la tecnología está dada. No sería así de tener la posibilidad de incrementar los factores productivos que hemos  considerado fijos (aumentar el nº de hornos y/o alquilar otro local) o de mejorar la tecnología, que es lo que ocurre en el largo plazo.

Al punto donde PMe = PMg se le conoce como óptimo técnico. Este punto es importante porque nos indica cuándo empieza a actuar la ley de los rendimientos decrecientes pero ojo, NO señala dónde alcanza su máximo la función de producción. La función de producción alcanza su máximo cuando la productividad marginal del factor variable (trabajo) es 0.

B. LA PRODUCCIÓN A LARGO PLAZO

En términos de producción, se considera largo plazo el periodo de tiempo en el que la empresa puede variar todos los factores que utiliza, de forma que ningún factor es fijo. En el ejemplo de la pastelería, a largo plazo no habría factores fijos: podríamos alquilar un local más grande u otros locales, utilizar hornos con más capacidad o en mayor número, recurrir a formas alternativas de organizar la producción e incluso introducir mejoras tecnológicas.

En definitiva, a largo plazo, el elenco de opciones que se le abren a cualquier empresa para acometer el proceso productivo son mucho mayores, ya que todos los factores pueden variar.

De este modo, si quisiéramos seguir aumentando progresivamente la producción de la pastelería o de cualquier empresa, tendríamos que hacerlo incrementando tanto el trabajo como el capital y eso, como hemos visto, sólo podríamos hacerlo a largo plazo, para lo cual tendríamos que variar la escala en la que utilizamos los factores productivos.

Si variamos todos los factores utilizados en la misma proporción obtendremos una cantidad de producto a la que se denomina rendimiento de escala. Por tanto, los rendimientos de escala miden la variación del producto total cuando se aumentan proporcionalmente todos los factores. De ahí que podamos encontrar:

• Rendimientos de escala crecientes o economías de escala. Cuando al variar la cantidad utilizada de todos los factores en una proporción determinada, la cantidad obtenida de producto varía en una proporción mayor.

• Rendimientos de escala constantes. Cuando la cantidad utilizada de todos los factores y la cantidad de producto obtenida varían en la misma proporción.

• Rendimientos de escala decrecientes o deseconomías de escala. Cuando al variar la cantidad utilizada de todos los factores en una proporción determinada, la cantidad obtenida de producto varía en una proporción menor.

Para ilustrar estos conceptos utilizaremos de nuevo el ejemplo de la pastelería. Partimos de una situación inicial en la que con dos hornos y cuatro trabajadores se alcanzaba una producción de 800 pasteles. Supongamos ahora que la pastelería incrementa sus factores productivos en un 100%, de tal forma que dispone de 4 hornos y 8 trabajadores. Por tanto, dependiendo del nivel de producción que alcance en esta nueva situación, podremos determinar si la pastelería presenta rendimientos de escala constantes, crecientes o decrecientes: